投資計算では、確定拠出年金や年金資産運用のための、情報発信をしている。

　投資信託、いったい何を選べばいいのだ。結論から先にいえば、４５歳までは、NYダウインデックスファンド１００％。これで全く問題ない。選択できる商品にNYダウインデックスがなければ、外国株式でもよい。「え〜、そんな〜、分散投資しないとリスクが高い、と投資教育で習いました。リスクが高いと、元本割れの危険性が高いそうです」という声が聞こえてきそうだ。確かに「リスク＝標準偏差」ということであれば、外国株式はリスクが高い。ただ、リスクが高いというこは、元本を下回る確率が高いということではない。この辺を勘違いしている人が多い。　

　弊社が計算した結果、今、外国株式インデックスファンドを購入した場合、１５年後に元本を下回る確率は 1.1%。２０年後になると0.06%だ。元本保証みたいに見えるではないか。
　1985年1月から2018年12月までのデータを使って確認してみた。購入してから15年経って、元本を下回ったことは一度もない。

　ついでに、外国債券インデックスファンドが元本を下回る確率を計算してみた。15年後2.9%、20年後0.8%。そう、ハイリスクハイリターンのファンドの方が、長期運用になると元本を下回る確率が、小さくなるのだ。これで、外国株式の期待リターンは6.8%。外国債券の期待リターン4%。どちらが魅力的に見えるだろうか。

　そんな話は聞いたことがないって？・・そりゃそうだ。私も、他の人や団体がこのようなこと言っているのを聞いたことがない。そもそもリスク（標準偏差）と期待リターンから元本を下回る確率を計算した例を見たことがない。

　このサイトは、上記について詳しく述べていく。また、投資教育の嘘も指摘していく。話は細かくなってしまうが、せっかくこのサイトにたどり着いたのだから、しばらくお付き合いいただきたい。

平成31年2月更新

　　　　　

外国株式の特長

リーマンショックの時は、1/3までさがった。

まず、外国株式の価格変動を見てみよう。正確に言うと、MSCI　KOKUSAIインデックスで、1985年1月を100としたものだ。円に換算してある。

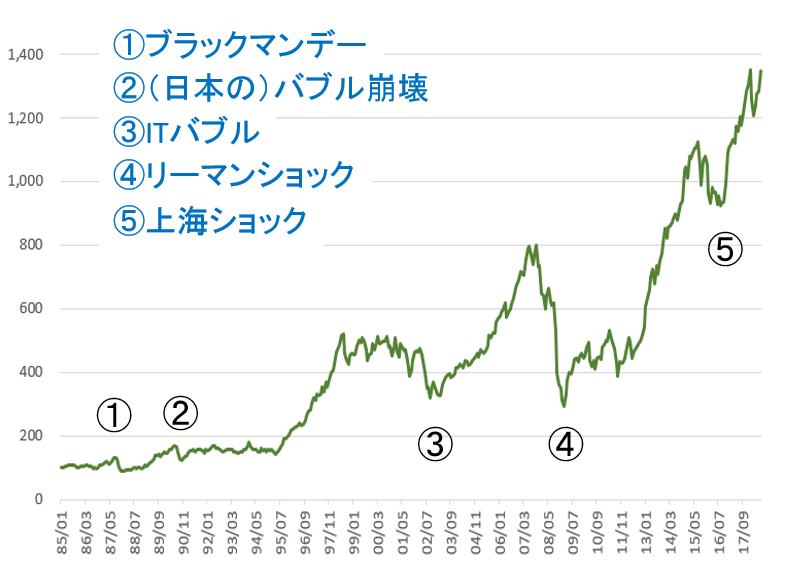
ぱっとみて分かるのは、リターンが大きい　ということだ。1985年に100が、2018年7月1346となっている。

騰落がおおきい。つまり暴落がある。ひどい時は、リーマンショックの時のように、1年4か月で3/1近くになることもある。33年で5回。単純計算すると6年に1度の割合だ。
（暴落の定義は曖昧だ。ここではグラフを見て目だっているところを暴落としている）

1. ブラックマンデー　　　　　4か月　67％
2. （日本の）バブル崩壊　　　3ヶ月　75％
3. ITバブル　　　　　　　4年2ヵ月　62％
4. リーマンショック　　　1年4ヶ月　36％
5. 上海ショック　　　　　1年2ヶ月　84％

平成31年2月26日更新

　

15年後に、元本を下回ったことはない。

暴落しても、いずれ回復する。回復する期間は、長かったり短かったりする。暴落前ののピークから。そのピークの値にもどして、その値を下回らないようになる期間を調べてみた。

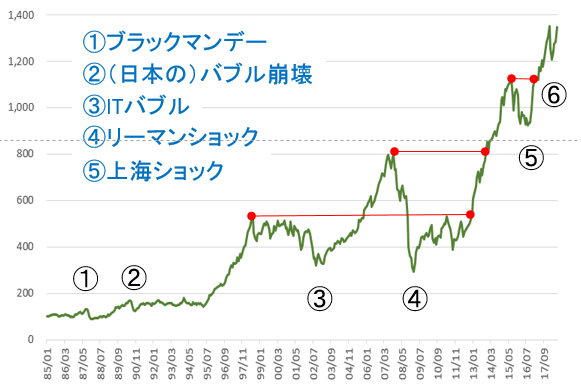
1. ブラックマンデー　　　　　1987年8月〜1989年7月　　1年11ヶ月
2. （日本の）バブル崩壊　　　1990年6月〜1995年8月　　5年2ヶ月
3. ITバブル　　　　　　　　　1998年7月〜2012年12月　14年5ヶ月
4. リーマンショック　　　　　2007年10月〜2013年11月　6年1ヶ月　
5. 上海ショック　　　　　　　2015年7月〜2017年3月　　1年8ヶ月

バブルのあと、リーマンショックでもう一度たたき落されて、復活するのに14年5ヶ月もかかってしまった。逆に考えると、1985年以降のどの月でもいいのだが、外国株式を購入して14年5ヶ月そのまま持っていた場合、購入時よりも下がることは一度もなかったということだ。

外国株式の基準価格がこれまでと同じような変動をすると仮定すると15年後の基準価格が現在よりも下回るという確率は、とても低いと考えられる。

平成31年2月26日更新

運用結果は正規分布する。

　運用結果が正規分布すると仮定できれば、確率が計算できる。

　運用結果が正規分布する、と仮定できるのであれば、一定の範囲内の確率が計算できてしまう。例えば、10年後に元本を下回る確率は1.1％とか。とっても便利な法則なのだ。その確率を計算するのに必要なのは、期待利率と標準偏差の２つだけでいい。その２つは、過去の変動と経済状況から推定できる。

　ここでは、過去のデータをもとにして、本当に正規分布と仮定できるのか、確認する。。
　実際に1年間運用してみると、運用結果はプラスになったり、マイナスになったりする。
　1985年1月を100として、1986年1月までは、104.9
　1985年2月から1986年2月までは、104.6
　　上記のように1ヶ月ずつずらしていく
　2016年4月から2017年4月までは、115.2
　全部で376のサンプルがとれる。それをヒストグラム（度数分布を示すグラフ）で表示する。

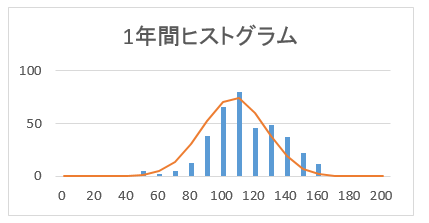
　棒グラフは、ヒストグラム。折れ線グラフは期待リターン6.8％標準偏差20％の理論値。きれいに重なっているではないか。正規分布している。念のため、10年、15年、20年、25年と長期間で確認してみよう。

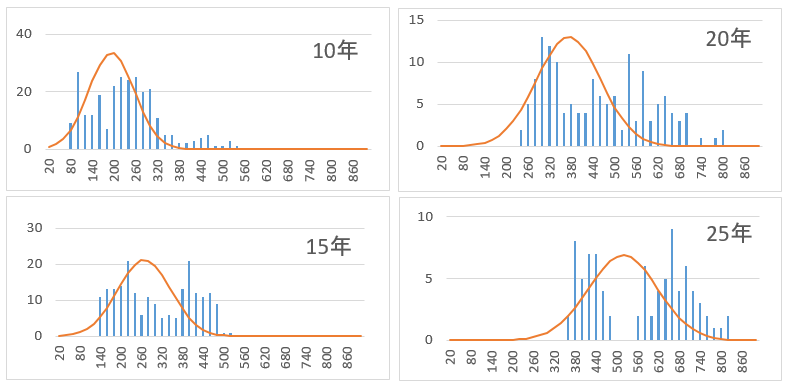
　長期になると、２こぶになる傾向がみえるが、正規分布すると仮定できるだろう。

平成31年4月16日更新

正規分布の平均は複利計算　リスク（標準偏差）は　√N

　確率計算する前に、1年後の予測をする。

　外国株式の期待リターンを、6.8％。リスク（標準偏差）を20％とする。
　1985年1月から2019年1月までの、実測値は　リターン7.7％　標準偏差17.4％
　ここではリターンは、1年複利で計算してある。
　将来予測のための期待リターンと標準偏差は、過去のデータを参考にしながら、決める。

1年後の予測
　少々細かいが計算式を書いておく。

• 中心値　　　　　　 100万×　1.068　　　　 ＝107万円
• －1σ　　　　　　　100万×（1.068－0.20）＝87万
• ＋1σ　　　　　　　100万×（1.068＋0.20）＝127万
• －2σ　　　　　　　100万×（1.068－0.20×2）＝67万
• ＋2σ　　　　　　　100万×（1.068＋0.20×2）＝147万

　－1σから＋1σの間に入る確率は68％。
　－2σから＋2σの間に入る確率は95％

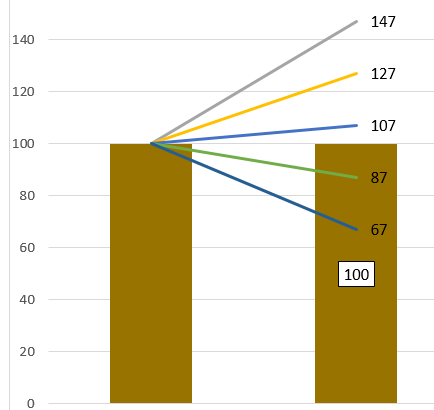
　100万円用意して、6万8千円の利益をねらう。
　その結果、100万円が87万円に、つまり損害が13万円を越えるる確率は、
　16% 　（100%-68%)/2=16％
　自分にとって、いいのか、悪いのか微妙なところだ。確率で言ってもピンと来ないかもしれない。
　実際の投資教育の中では、このような説明をすることがある。

　この説明が問題なのは、2年後の説明をしないことだ。想像をたくましくすれば、開き方が、そのまま直線的に進み、それこそ3年後になれば100万円が０円になってしまうことが、少なからずありそうに見えてしまう。ましてや、10年後、20年のことは、想像できないと、思考を停止してしまう人が、ほとんどではなかろうか。

　2年後の予測をする。（10年後、20年後はさておき）

• 中心値　　　　　　 100万×　1.068²　　　　 ＝114万円
• －1σ　　　　　　　100万×（1.068²－0.20×√2）＝86万
• ＋1σ　　　　　　　100万×（1.068²＋0.20 ×√2 ）＝142万
• －2σ　　　　　　　100万×（1.068²－0.20 ×√2 ×2）＝57万
• ＋2σ　　　　　　　100万×（1.068²＋0.20 ×√2 ×2）＝171万

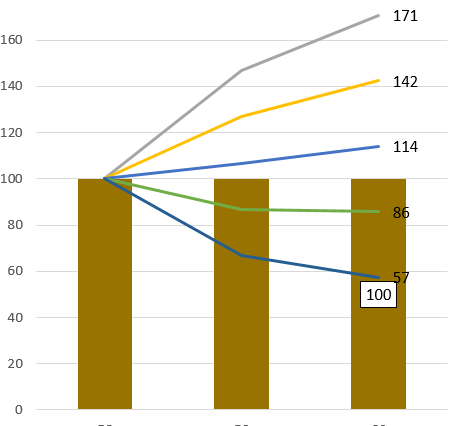
中心値は1年複利計算　 ←　増え方が増える
σは√N（年）をかける　←　増え方が減る

　株式指数の変動は、正規分布すると仮定できる。そのことは、前項で述べた。
　正規分布するのであれば、この計算式が摘要できる。
　将来予測や、確率計算にとってこの計算方法は重要なのだ。

　現在の資産配分で、退職時点での元本割れ確率を計算できる。

　令和元年5月28日更新

将来予測は、バナナカーブ

前項で、2年後の予測をした。その計算方法も示した。ここまでくれば、10年後、20年後の予測は簡単だ。まず10年後のグラフを示す。

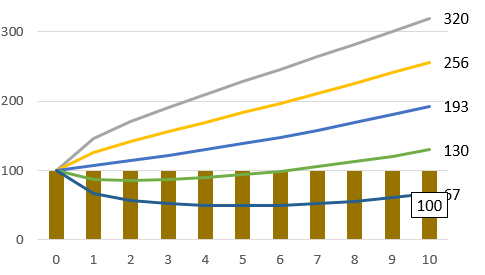
10年後

10年後のグラフ。慎重な人には、抵抗があるかもしれない。-2σの曲線が、50万くらいまでいったん下がってしまうのは、いやな感じだろ。
ちなみに、表題につけた「バナナカーブ」とは、このリスク（標準偏差）曲線を私が勝手に付けた名前で、一般的に通用する言葉ではない。

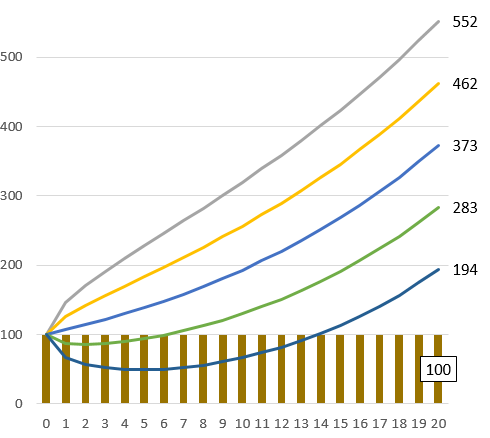
20年後

20年後のグラフ。-2σで194万だ。-3σでさえ元本の100万を上回っている。元本割れ確率を計算すると、たった0.11％だ。退職までに20年以上ある人、「ここ、大切なところですよ」２０代、30代の人が周りにいたら、この話をぜひ伝えてほしい。世の中には、
「外国株100％はリスクが高いのでやめておいた方がいい。なぜならば、元本を下回る危険性が高いからだ。」
と、親切に忠告してるれる人がいる。その時には確認してほしい。
「何年後の話ですか。元本を下回る確率はどのくらいですか？」と。

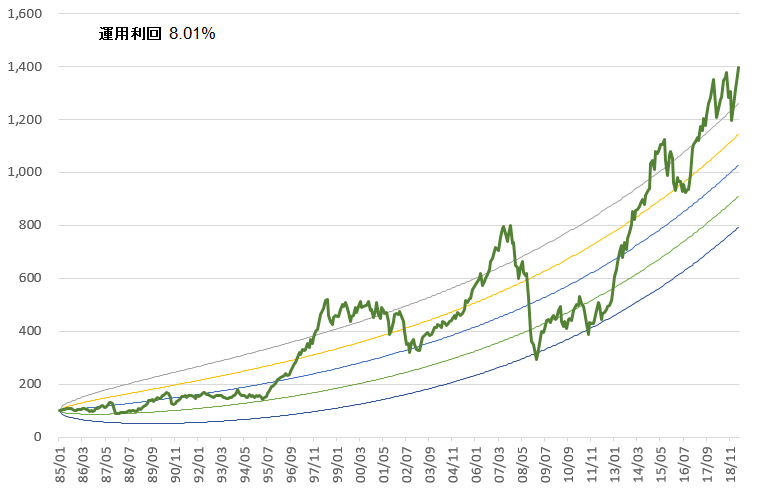
外国株株式指数の変動と、バナナカーブ

外国株式指数（MSCI KOKUSAI)とバナナカーブを重ねて表示してみた。美しい・・？。
（数値を加工してグラフを作っているときに、結果をみて自己満足に浸れることがあるが、このグラフはそれだ）
　過去の指数からリターンと標準偏差を計算して、ちょっとだけ手を加えて、グラフを重ねているのだから、きれいに重なって見えるのは当然なのだが。
バナナカーブの元となる数値は、期待リターン6.8％　リスク（標準偏差）20％
実際の価格変動から導かれるのは、リターン8.01％、リスク（標準偏差）１7.38％
（1985年1月〜2019年4月）
-2σから＋2σの間から、そうそう、大きく外れないと、思ってしまうような結果だ。

このグラフは、開始時期をいつに設定するかによって、大きく見え方が違う。導きたい答えを誘導するのに適した開始時期や終了時期を見せることができてしまう。
なので、最悪の時、リーマンショックの直前からグラフを始めてみた。

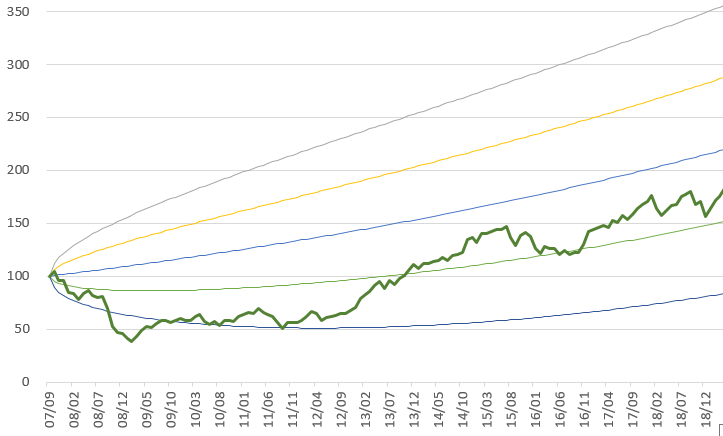
おお、3か月後に-2σを飛び出している。飛び出したままにならないところが、このグラフのいいところともいえる。
いろいろなグラフを見て、自分なりに長期投資における株価の変動の特長をつかんでほしい。

令和元年6月18日更新

長期運用、元本割れ確率は下がり続ける。

　世界株式の長期運用。いったい何がいいのか。ずばり、元本割れ確率が下がり続けることだ。「15年後に元本を下回ったことはない。」と既に書いた。15年後に元本を下回る確率は、1.5％だ。30年後に至っては、7.7E-7％・・限りなく0％に近いとでも言っておこう。

　確率を計算する方法を説明する。1年後の外国株式の運用結果は、左下の図のように正規分布する。頂点は106.8と右に移動する。グラフの底辺はリスク（標準偏差）から計算できる。2年後、右下図のように、頂点は右に移動し、底辺はさらに広がる。頂点は複利計算、リスク（標準偏差）は√Nをかける。
　下の図の元本100の左側を水色に塗ってみた。山の全体の面積のうちの水色の面積の割合が、元本割れ確率となる。1年後と2年後。2年後の方が水色の面積が減っているのだが、わかってもらえるだろうか。

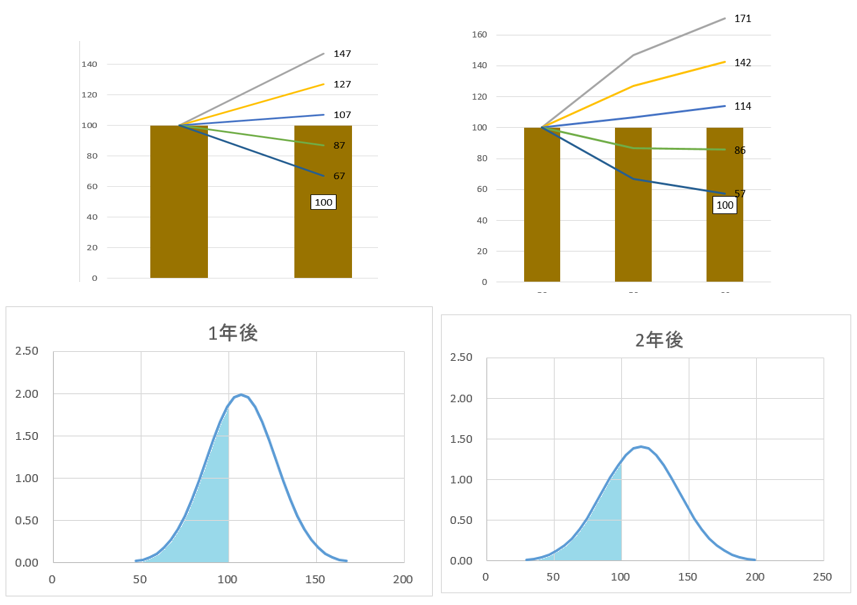
　詳細な計算方法は、ここでは省略（実は知らない）
　エクセルには、平均値と標準偏差から、確率を計算する関数がある。
　=NORMDIST(値,平均,標準偏差,TRUE)　（累積分布関数の値を求める場合はTRUE）

　例として、2年後の元本割れ確率を関数を使って計算してみよう。
　期待リターン6.8％　リスク（標準偏差）20％とする。
　=NORMDIST(100,100*(1+0.068)^2,20*SQRT(2),TRUE)
　このままエクセルのセル（枠）に貼り付けてもらえば、0.30953と表示されるはずだ。
　つまり30％。^2 と　SQRT(2) の 2 の部分をそのまま増やしていけば、将来の元本割れ確率が計算できる。グラフにしてみよう。

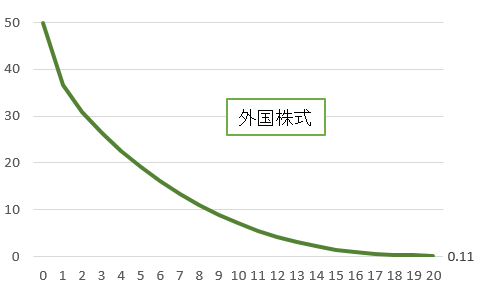
　10年後の元本割れ確率7.1％。15年後は1.5％。20年後の確率は、0.11％
　このように、元本割れ確率は、下がり続ける。

令和元年6月29日更新

長期運用、リスク（標準偏差）は増え続ける

　前の方の鴻で、N年後のリスク（標準偏差σ）は√Nをかける、と書いた。また、バナナカーブで、-σから＋σの間隔が、広がっていくことも確認した。期間とともに、リスク（標準偏差）が増えていくことは、当たり前なのだ。

　前回は、「元本割れ確率が下がる」今回は、「リスク（標準偏差）が増える」矛盾しているようだが矛盾していない。言葉の定義をしっかりとらえてもらいたい。「長期運用は収益が安定する」などと、言葉の定義があいまなまま、信じてしまっていたら、「長期運用、リスクは増える」と言われたときに混乱するだけだ。

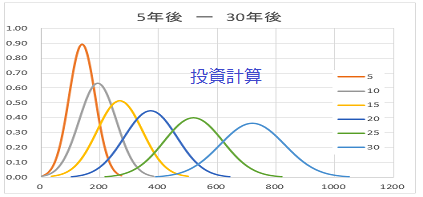
　数式で説明しても分かりにくいかもしれないので、グラフを作成してみた。
期待リターン6.8%、リスク（標準偏差）20%の、5f年後から30年後までの5年間隔で分布図を示す。

　

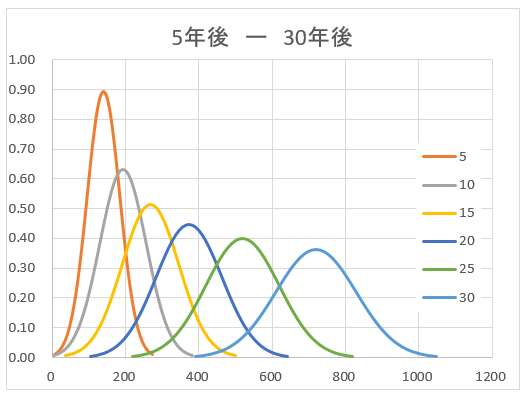
　5年後は、一番左の橙色の曲線。その後5年ごとに頂点（平均）は右に移動し、すそ野は徐々に広がっている。このすそ野の幅が、リスク（標準偏差）を表現している。
　長期運用の運用結果は、リスク（標準偏差）は増えるのだ。

　ちなみに、グラフの線は、-3σから+3σまで書いてある、この間に入る確率は、99.7%だ。もし、-3σより下回ってしまったら、アンラッキーだと思ってあきらめよう。

令和元年7月2日更新

長期運用、リスク(標準偏差)の高いほうが,元本割れ確率は低い

　「ハイリスク・ハイリターンの商品は、危険性が高い・・？。」投資教育を提供する立場になって、投資教育を受講することがなくなってしまったが、今でもこのフレーズは、使われているのだろうか。何となく分かってしまったような気分になるフレーズである。「危険性」とは何か。まず「危険性」の意味を定義しなければ、何を言っているのかわからない。

　ここでは、「危険性が高い」を、「元本割れ確率が高い」と定義する。具体的な資産の期待リターンと、リスク（標準偏差）で確率を計算し、比較してみる。

　日本債券、外国債券、外国株式の3つ。
　日本債券　期待リターン0.5%　リスク（標準偏差）1.9%
　外国債券　期待リターン4.0%　リスク（標準偏差）11.0%
　外国株式　期待リターン6.8%　リスク（標準偏差）20.0%
この数値は、普段から、私がシミュレーションで使っている数値だ。違うご意見があっても全く問題ない。横軸標準偏差、縦軸期待リターンで示す。

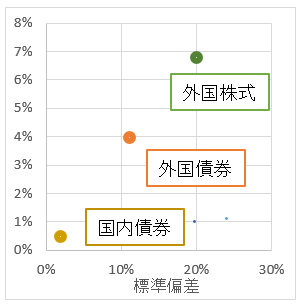
　次に元本割れ確率曲線を描く。エクセルのNORMDIST関数を使えば簡単だ。
　使い方は、「長期運用、元本割れ確率は下がり続ける」に既に書いた。。

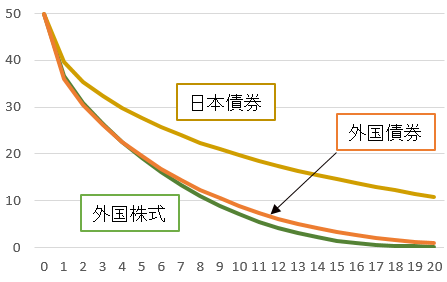
　なんてことだ。元本割れ確率が一番低いのが、外国株式、次が、外国債券、一番高いのが日本債券。
　もっと正確に言うと、5年後に外国株式の元本割れ確率が、外国債券より下回る。
　「ハイリスク・ハイリターンの商品は、危険性が高い（ここでは元本割れ確率が低い」が、常に成り立つわけではない。運用期間が短い場合にのみあてはまるのだ。長期運用では、ハイリスク・ハイリターンの方が、元本割れ確率が低くなる・・ということを、十分理解してほしい。

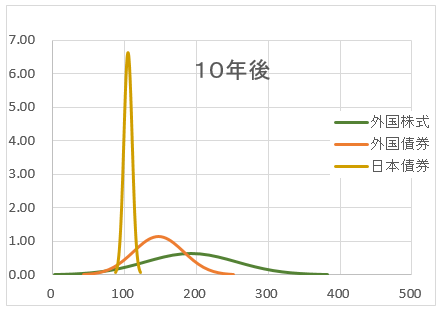
　上記グラフだけで、納得することは、難しいと思われる。次に、異なる３つの資産を異なる期間（1年後、5年後、10年後、20年後、30年後）の分布図を示す。（分布の範囲は、-3σから+3σ）

　　　　

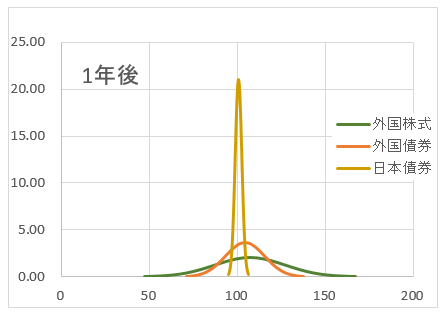
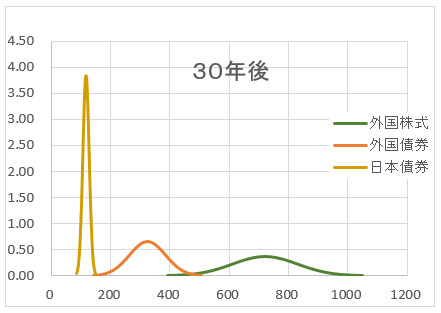
1年後のグラフ。外国株式の運用結果の範囲は、47〜167　平均値は107
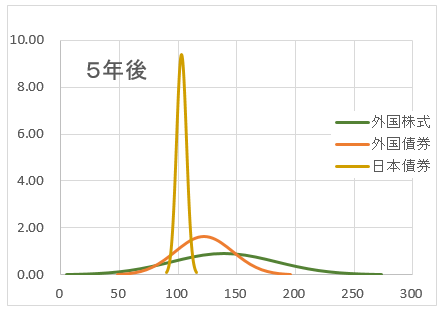
5年後のグラフ。外国株式の運用結果の範囲は、5～273　　平均値は139
どのような印象を持たれただろうか。
「運用結果の範囲、広すぎでしょ。このリターン（平均値）を狙うのに、危険を冒したくない。」
リスク（標準偏差）の中くらいの外国債券くらいならいいかな。」
このような印象を持たれる方が、多いのではないか。

途中を飛ばして
30年後のグラフ。外国株式の運用結果の範囲は、391〜1048　平均値は1048
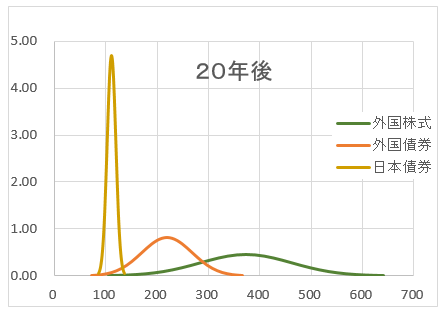
-3σの値が、外国債券の平均値324を超えているではないか。
このグラフだけを見れば、何が何でも外国株式と、感じるのではないだろうか。

　退職まで、20年以上ある20代30代の会社員で、外国株式100％を選択している人が、どれだけいるのだろう。投資信託の長期運用のメリットとして、このようなグラフを使い、元本割れ確率に注目しているサイトや書籍、投資教育を見たことがない。ここに訪れ、理解納得した人にお願いしたい。
「多くの人にこのサイトを教えてあげて。」

令和元年7月9日更新

長期運用、元本を30％以上下回る確率。

　投資について書いていると、他のサイトを見て、参考にしたりすることもある。。リスク・リターンの説明はどうなっているのか。（財）投資信託協会のサイトに、「大きな収益を期待すると、リスクが大きくなり、逆に大きな損失の可能性も増す」というのがあった。本当か。「リスク」「大きな損失」「可能性」ではあいまいなので、こちらで勝手に定義してみた。「リスク」は標準偏差。「大きな損失」は、元本より30％以上下回る運用。（大きな損失といわれると、何％の損失のことを頭に描くのか人によって違うと思うが、ここでは30％の損失とした）「可能性」は確率。まとめると、「期待リターンと、標準偏差の高い商品は、元本を30%以上下回る確率が、そうでないものに対して高い」という命題は成り立つのかどうか。いつものエクセルの関数を使って計算してみた。

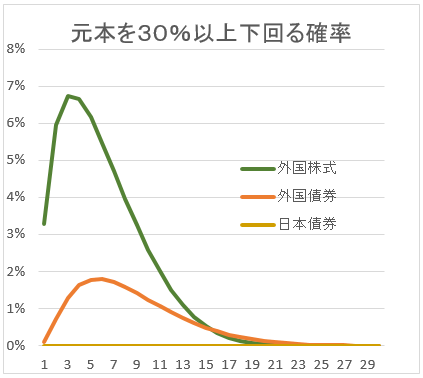
　確かに、ハイリスクハイリターンの外国株式のほうが、元本より30%以上下回る確率は高い。特に最初の方は。16年後には、世界株式と、世界債券が逆転する。日本債券はさすがにほとんど０である。
　前記の、命題が成り立つかと言えば、「常に成り立つとは言えず、長期においては、元本を30%以上下回る確率が、逆転することもある」というところだろうか。

　ついでに、40％以上、50％以上下回る確率も計算してみた。

　

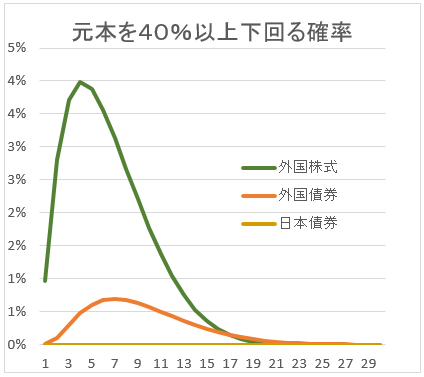
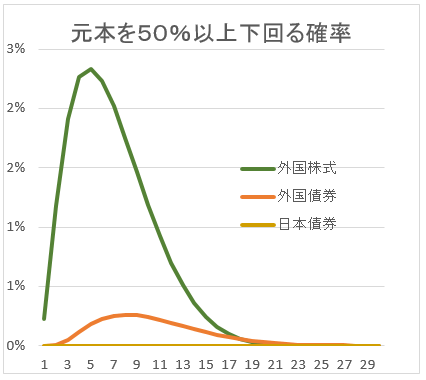
　確率の一番高いピークと、確率が逆転する年数が後ろにずれることが観察できる。　
　15年以上の長期運用では、あまり気にするな・・ということが、分かるのではないか。

　話は変わるが、、世の中の人は、「大きな収益を期待すると、リスクが大きくなり、逆に大きな損失の可能性も増す」というのと、「期待リターンと、標準偏差の高い商品は、元本を30%以上下回る確率が、そうでないものに対して高い」というのとでは、どちらが分かりやすい文なのだろう。文学的表現と、数学的表現とでもいうのだろうか。投資信託を説明するサイトは、文学的表現で、専門用語を使わずに分かりやすく？説明しているため、私には分かりにくく感じてしまうのである。

令和元年7月18日更新

リターンとリスク（標準偏差）の実績と、今後の予想
　　（日本株式、外国株式に比べリスクは同じでリターンは半分）

　懐かしい図を、以前使っていた資料から持ってきた。。一番ローリスクローリターンが元本確保商品で、一番ハイリスクハイリターンが外国株式。他の資産はその間にほぼ直線上に並んでいる。分散投資したほうが、リスクが下がるので、基本は、外国株式、国内株式、外国債券、国内債券を25％づつ。もう少しハイリターンを狙いたいなら、株式を30％ずつ。債券を20％ずつと、株式の比率を高めていけばいいですよ。などど説明したものだ。実際に自分の確定拠出年金を株式30％ずつ債券20%ずつで運用していたことがある。

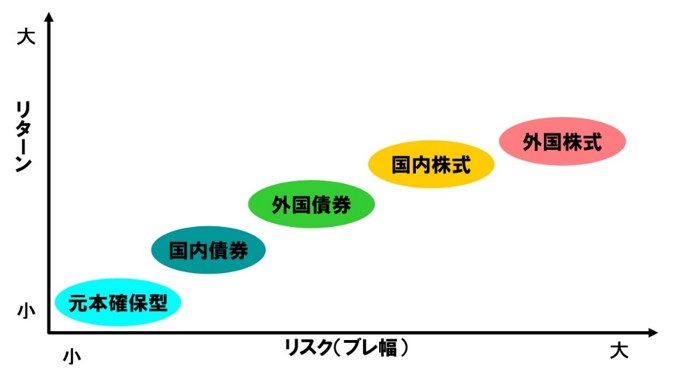
　だまされてはいけない。いや、だましてはいけない・・か。実際の各資産の変動はこのようにはならない。過去30年間、平成元年6月を100としたときの指数の変動を以下に示す。

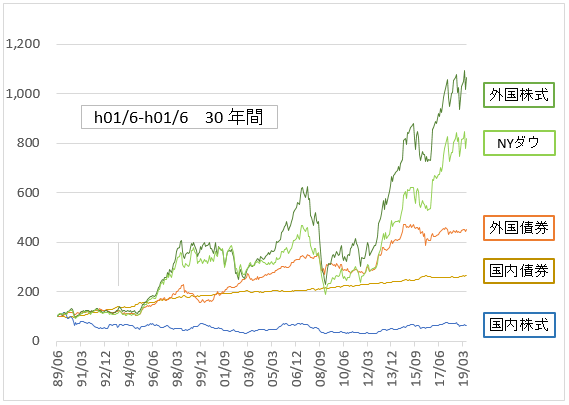
　外国株式10倍。国内株式63%（37%元本割れ）・・国内株式を選んではいけないのか？　
　折れ線グラフでは、評価しにくいので、リスクリターンの図で示す。横軸がリスク（標準偏差）。縦軸がリターン。令和元年6月末を固定して、過去30年、20年、10年、5年、3年、1年の6つのパターン。過去のインデックスデータを取り込んで、計算しないといけないので、手間のかかる作業ではある。

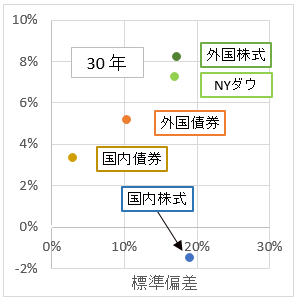
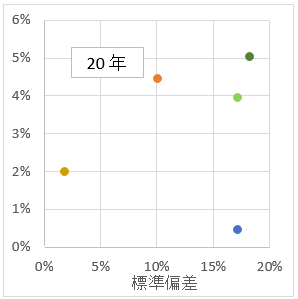
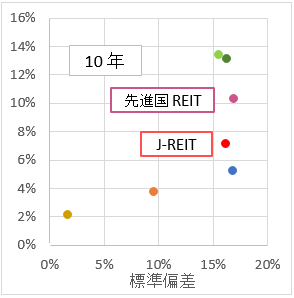
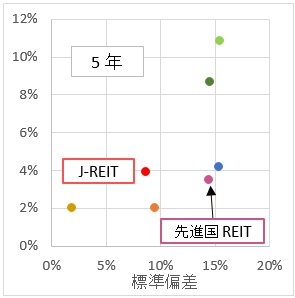
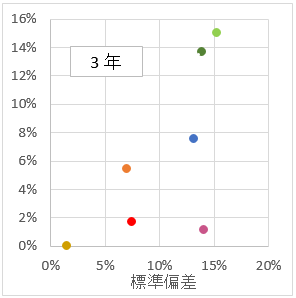
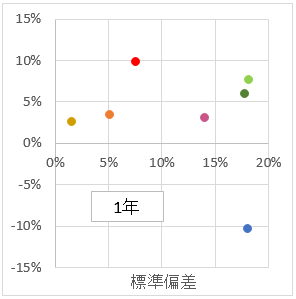
過去の実績をみて、全体的な傾向を掴んでみる。

• 外国株式が、リスクも、リターンも高い。
• 直近10年は、外国株式よりも、NYダウの方がリターンが高い。
• 国内株式は、外国株式とリスクは同じくらいだか、リターンは半分以下。
• 国内債券は、リスクもリターンも低い。
• 外国債券は、リスクもリターンも国内債券と外国株式の中間くらい。
• REIT・・

　過去の実績をみて鉛筆なめなめ作った将来予測が、下図である。2つあるのは、ラベルの有る無しだけの違いだ。意図的に少し、リスク（標準偏差）を高め、リターンを低めに作ってある。

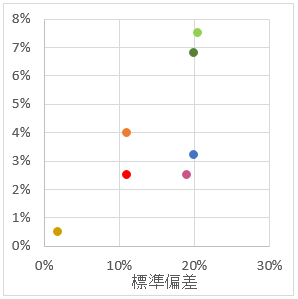
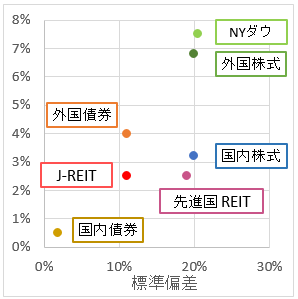
　この図から、気づいてほしいのは、分散投資の対象から、国内株式、国内REIT、先進国REITを外した方が良いということだ。リスクの割にリターンが低すぎる。その昔、外国株式100%を選択しようしている人に、「せめて国内株式に分散した方が安心ですよ。」などと、言ったことがあるように記憶している。間違いでした。外国株式に国内株式の割合を増やして分散投資するのは、リスクはそのままで、リターンが下がるだけだ。
　分散投資をする場合、過去の実績を踏まえ、リスク（標準偏差）もしっかり見て投資対象を決定しよう。
（分散投資した場合、リターンは各資産の加重平均でよいが、リスク（標準偏差）は相関係数を含めて計算するのが、正式な方法）

令和元年7月21日

名目GDPに引きずられる、株価指数　（G7名目GDPと株価指数の比較）

　世間の評価がどうであれ、弊社での日本株式の評価は低い。前項で述べたように、過去のほとんどの期間で、外国株式と比べ、リスク（標準偏差）は同程度で、リターンが低かったからだ。（それも半分以下）当然、将来の期待リターンは低くなってしまう。だがちょっと待て、「当然」と書いたが、本当に「当然」なのか。これまで、世界株式に比べリターンが低かったのには、何か原因があるのではないか。そして、その原因が今後取り除かれていくのであれば、日本株式は「買い」ではないか。

　ということで、名目GDPと株価指数の関係について調べみた。

• 名目GDPも、株価指数も、現地通貨で1970年を100とした。
• 株価指数について、カナダとイタリアは1970年からのデータが入手できなかった。
• 相関係数が高い順に並べた。

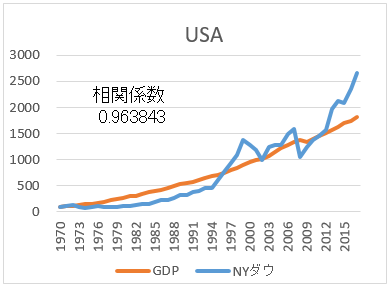
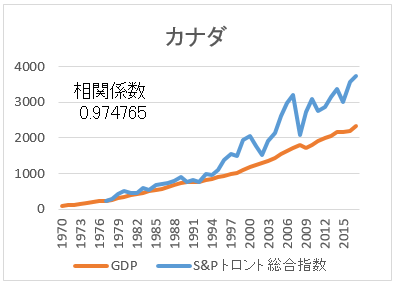
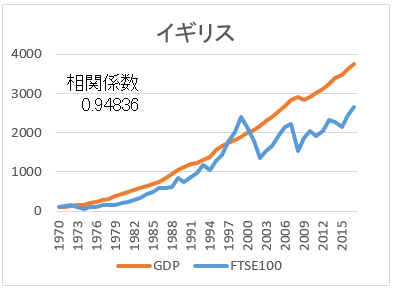
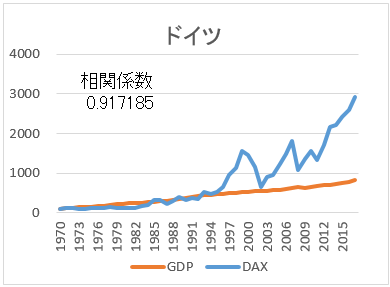
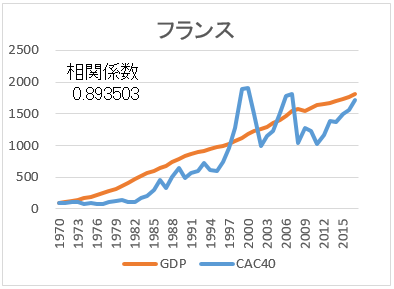
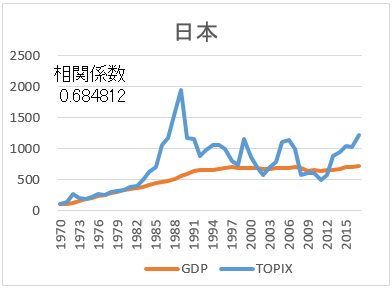
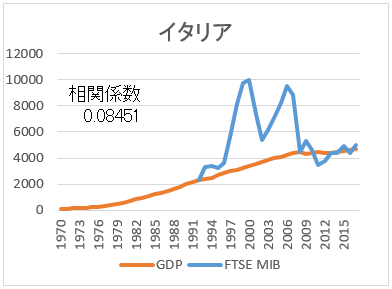
　まず、全体を見てほしい。見て分かることは、名目GDPと株価指数は、相関が高いということだ。つまり、経済成長していれば、株価指数も上がるのだ。次に、日本とイタリアはに注目してほしい。途中から経済成長が止まっている。そして、成長の止まっている名目GDPのグラフに引きずられる形で、株価指数も伸び悩んでいる。

　20年以上も経済成長の止まっている日本株式を、自国の株という理由だけで、わざわざ選択する必要はない。これまでと違って、他国並みに経済成長する・・というのであれば別だが。

令和元年8月28日更新

日本の経済成長は、世界最低。国別名目GDP成長率の比較

　「日本の経済成長は世界最低」、などと書くときは、そうなる期間を選択して、提示するのが一般的だ。今回の提示もその例にもれない。今回は1996年から2017年にかけて名目GDPが何倍になっているのかを比較してみた。経済成長率を他国と比較すると、興味深い現状が観察できる。
国際連合のデータを使った。
使い方は総務省の統計局が作ってくれている。http://www.stat.go.jp/data/sekai/pdf/sna.pdf　

　国連のサイトでは、214か国のデータがとれる。今回は1996年から2017年にかけて名目GDPが何倍になっているのかを比較してみた。その期間のデータが取れない国もあるので、データの取れる国だと208か国となる。

　その中で日本は、208番目　最下位。1.04倍
　ちなみに1位はアンゴラ。18,788倍。多分、とてつもないインフレ国家なのだろう。
　このような国を混ぜて、グラフを作ったところで縦軸のスケールがとんでもなくなるので、ここでは掲載しない。

　次に、G7か国に中華人民共和国と韓国を加えて9か国のデータでグラフを作ってみた。

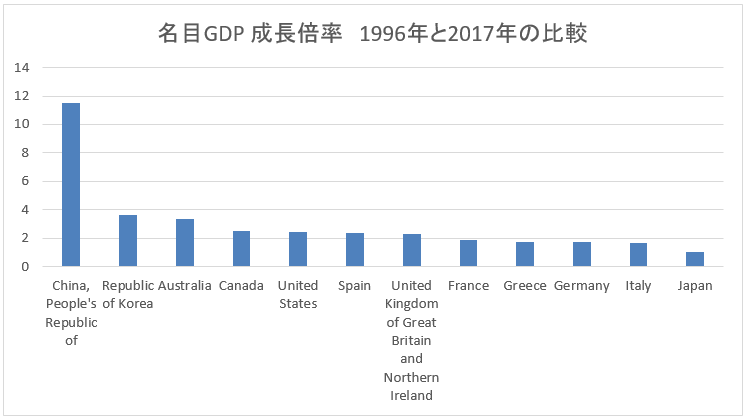
　先進国は、だいたい、2倍前後。アメリカは、2.41倍。下から2番目のイタリアでさえ1.65倍。
　そして中国は、11.5倍。韓国でさえ3.6倍。
　何度も書くが、名目GDPと株価指数の相関は高い。わざわざ、経済成長をしていない国の株を買う必要はない。

　さて、ここまでは過去の話だ。この世界最低の経済成長の原因は何か。その原因が取り除かれて、他の先進国同様の経済成長が見込まれるのであれば、「買い」でも良いはずだ。

令和元年10月14日更新